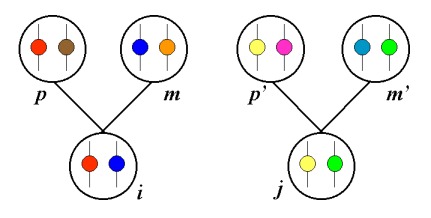
Calcul des coefficients de parenté par la méthode tabulaire

L'idée de base de la méthode tabulaire est de noter que les deux gènes présents chez un individu quelconque proviennent respectivement d'un tirage au sort parmi les deux gènes présents chez son père, d'une part, et d'un tirage au sort parmi les deux gènes présents chez sa mère, d'autre part (voir le schéma ci-dessous).

Les probabilités d'identé des gènes entre deux individus donnés peuvent donc se déduire des probabilités d'identité à l'échelon parental. Soit p et m le père et la mère de i, p' et m' le père et la mère de j, alors :

L'équation 3 n'est cependant valable que si aucun des deux individus (i ou j) n'est parent de l'autre :

• Si i est parent de j, on applique l'équation 2.
• Si j est parent de i, on applique l'équation 1.

Par ailleurs, cette méthode implique souvent le calcul du coefficient de consanguinité d'un individu avec lui-même. En revenant aux définitions de base, on montre que ce coefficient (F_ii) s'exprime en fonction du coefficient de consanguinité de i (F_i), qui n'est autre que le coefficient de parenté entre son père (p) et sa mère (m) :

   NB. Avant de passer à des exemples, il peut être utile d'imprimer cette page.