Méthode tabulaire Mise en oeuvre pratique et comparaison avec la méthode des chemins

La méthode tabulaire, du fait de sa simplicité, est bien adaptée à un taitement informatique des données. Dès lors que l'on vise des applications de grande taille (concernant un grand nombre d'individus), il est recommandé d'appliquer cette méthode. En effet, la méthode "des chemins" induit des temps de calcul généralement plus importants et, du fait d'une plus grande complexité, il y a plus de risques d'erreur au cours de sa programmation. Les paragraphes qui suivent indiquent la procédure à suivre.

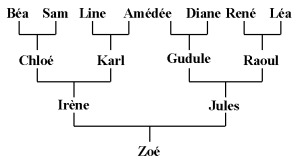
1) Le point de départ réside dans la constitution d'un fichier généalogique, qui comprend 3 colonnes dans lesquelles on fait fugurer les informations suivantes : (1) identité de l'individu, (2) identité de son père et (3) identité de sa mère. Il convient de classer les individus du fichier par âge décroissant, afin que, au cours de la lecture du fichier, les parents soient rencontrés avant leur(s) descendant(s). Par exemple, pour le pedigree de Zoé (rappelé ci-dessus), on constitue le fichier suivant :
 

 
Un "blanc" dans une des deux colonnes "père" ou "mère" signifie que le parent en question est inconnu. Pour un traitement informatique, on remplace les noms par des numéros, un parent inconnu étant désigné par zéro :
 

2) On prépare ensuite une matrice de coefficients de parenté, c'est-à-dire un tableau qui comprend autant de lignes et de colonnes que d'individus enregistrés dans le fichier (dans l'exemple ci-dessus, 14 donc). Dans chaque case de cette matrice, viendra s'inscrire le coefficient de parenté entre les individus correspondants : par exemple, à l'intersection de la ligne 12 et de la colonne 5, se situe le coefficient de parenté entre les individus numérotés 12 et 5 respectivement (Irène et Diane). Une fois remplie, cette matrice est symétrique (F_ij = F_ji) et sa diagonale comprend les coefficients de parenté des individus avec eux-mêmes [F_ii].

3) La matrice est ensuite remplie de proche en proche (ligne par ligne), en démarrant par les individus les plus anciens :

• 1 avec lui-même.
• 2 avec 1, 2 avec lui-même.
• 3 avec 1, 3 avec 2, 3 avec lui-même.
• etc.

A une étape donnée, les coefficient recherchés sont calculés en appliquant les équations ci-dessous, étant entendu que tous les coefficients nécessaires ont été préalablement calculés, du fait de l'ordre retenu pour le fichier généalogique :

• Pour i et j différents (la matrice des coefficients étant symétrique, on ne considère que les cas où i > j) : Eq.1 de la page précédente.
• Pour i avec lui même : Eq.4 de la page précédente, le coefficient de consanguinité de i (F_i) étant égal, par définition, au coefficient de parenté entre ses parents.

4) Il est intéressant dans cette perspective de placer en haut du fichier généalogique tous les individus sans parents connus, qui constituent ce que l'on appelle généralement la population de base. En effet, en absence d'autre information, ces individus sont supposés non apparentés entre eux et non consanguins eux-mêmes. On isole alors dans la matrice des coefficients de parenté une sous-matrice concernant les individus de la population de base, qui a une structure particulière :

• Cette sous-matrice a autant de lignes et de colonnes qu'il y a d'individus dans la population de base (7 dans l'exemple d'Irène et Jules).
• Tous les termes hors diagonale sont nuls (non apparentement).
• Tous les termes de la diagonale valent 1/2 (non consanguinité).

Remarque importante

Telle que présentée ci-dessus, l'application de la méthode tabulaire requiert le calcul de tous les coefficients de parenté pour tous les individus du pedigree. Ceci peut engendrer une inflation du temps de calcul et un volume excessif de données à stocker. Aussi, sur le principe de la méthode tabulaire, plusieurs algorithmes de calcul rapide des coefficients de consanguinité ont été mis au point, visant, sans aucune approximation, à limiter les calculs au strict nécessaire (voir les références au sommaire général). Ces méthodes permettent ainsi de traiter dans des temps raisonnables des fichiers de plusieurs millions d'individus.