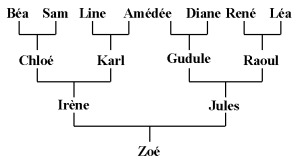
Méthode tabulaire Application au cas d'Irène et Jules

Irène et Jules n'étant pas parent direct l'un de l'autre, nous pouvons appliquer l'équation 3 de la page précédente :

Notons que, au vu de ce pedigree, Karl et Raoul n'ont pas d'ancêtre commun, de même que Chloé et Raoul et que Chloé et Gudule. Soit,

et donc,

Nous appliquons à nouveau l'équation 3 de la page précédente pour calculer le coefficient de parenté entre Karl et Gudule, en remarquant que ces derniers ont le même père (p = p' = Amédée) :

Pour calculer le coefficient de parenté d'Amédée avec lui-même, nous appliquons l'équation 4 de la page précédente, en considérant que, au vu du pedigree connu, Amédée est non consanguin (F_a = 0) :

Les autres coefficients sont nuls car les individus concernés n'ont pas d'ancêtre commun connu. Nous obtenons alors pour Karl et Gudule :

et donc, en définitive, pour Irène et Jules :

Notez cette valeur avant de passer à la suite. Ceux qui sont passé auparavant par la méthode "des chemins" peuvent vérifier que l'on retrouve ici la même valeur.