Méthode des chemins : un exemple pour se mettre en jambes

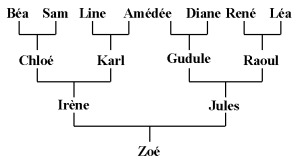
Reprenons le cas d'Irène et Jules, vu en introduction. Nous redonnons, plus bas, le pedigree connu de ces deux individus. Par définition, calculer le coefficient de parenté entre Irène et Jules, revient à calculer la probabilité pour qu'en un locus neutre quelconque, un gène tiré au hasard chez Irène soit identique par descendance à un gène tiré au hasard chez Jules. Soit, en désignant l'identité par le symbole "" :

Notre connaissance des généalogies s'arrête à la génération grand-parentale. En l'absence d'autres informations, nous devons considérer que tous les individus de cette génération grand-parentale sont, sur la plan génétique, indépendants deux à deux. En d'autres termes, tous les gènes qu'ils possèdent sont deux à deux non identiques par descendance (on suppose qu'ils proviennent d'ancêtres tous différents). Ainsi, Irène et Jules ne peuvent avoir reçu de copie d'un même gène qu'en provenance d'Amédée, qui est leur unique ancêtre commun.

A ce stade, il est utile de raisonner en termes de probabilités d'origine des gènes. Le raisonnement peut se suivre en 3 étapes.

1) En un locus quelconque, un gène d'Irène a une chance sur deux de provenir de Chloé et une chance sur deux de provenir de Karl. En remontant plus loin dans le pedigree, il est facile de voir qu'un gène d'Irène a une chance sur quatre de provenir de chacun de ses 4 grands-parents. En appliquant le même raisonnement à Jules, nous obtenons :

Le tirage d'un gène chez Irène étant indépendant de celui d'un gène chez Jules, nous avons :

2) Dans le cas où les deux gènes tirés proviennent d'Amédée, il faut déterminer la probabilité pour qu'ils soient identiques, c'est-à-dire pour qu'ils soient chacun la copie d'un même gène de cet ancêtre. Cela revient, dans le cas présent, à examiner les différentes combinaisons relatives à la transmission par Amédée d'un de ses gènes à Karl (père d'Irène) et à Gudule (mère de Jules). Les quatre situations suivantes sont équiprobables (Pr = 1/4)  :

• Amédée a transmis son gène paternel à Karl et son gène paternel à Gudule
• Amédée a transmis son gène paternel à Karl et son gène maternel à Gudule
• Amédée a transmis son gène maternel à Karl et son gène paternel à Gudule
• Amédée a transmis son gène maternel à Karl et son gène maternel à Gudule

On voit que dans le premier et le dernier cas, Amédée a transmis la copie du même gène (paternel ou maternel, peu importe) à Karl et à Gudule. La probabilité recherchée vaut donc 1/4 + 1/4 = 1/2.

3) Pour que les deux gènes tirés chez Irène et chez Jules soient identiques, il faut en définitive qu'ils proviennent tous deux d'Amédée et, sachant cela, que nous soyons dans la situation où c'est la copie du même gène qui a été transmis par Amédée à Karl et à Gudule. La probabilité d'un tel évennement, égale par définition au coefficient de parenté entre Irène et Jules, est donc égale au produit des deux probabilités calculées plus haut :

Cette valeur, que l'on peut également exprimer en pourcentage (3,125%) représente aussi le coefficient de consanguinité de Zoé. Notez cette valeur et passez à une présentation générale de la méthode "des chemins", en démarrant par la définition d'une chaîne de parenté.