Méthode des chemins Démonstration de la formule pour une seule chaîne de parenté

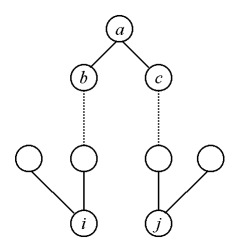
Soit i et j reliés entre eux par une seule chaîne de parenté passant par leur seul ancêtre commun a (cf. le schéma ci-dessus). On rappelle que le coefficient de parenté se définit pour un locus neutre sans mutation et s'exprime ainsi :

Les deux gènes tirés au sort, l'un chez i, l'autre chez j, ne peuvent être identiques par descendance que s'ils proviennent tous deux de a. Soit, en conditionnant par l'origine des deux gènes tirés au sort :

Les deux gènes tirés ne peuvent provenir de a que si, effectivement, i et j ont chacun reçu un gène qui était présent chez a. Nous décomposons donc la probabilité de tirer deux gènes provenant de a, et l'on obtient :

      [Eq.1]

Calculons successsivement les trois probabilités apparaissant dans cette équation.

1) Nous savons que les individus b et c ont automatiquement reçu chacun un gène de a (qui est leur père ou leur mère). Nous savons aussi que tout individu ayant reçu une gène donné d'un de ses deux parents directs n'a qu'une probabilité de 1/2 de le transmettre à un quelconque de ses descendants directs (aléa de la méiose). Soit n₁ le nombre total de maillons entre a et i (un maillon est représenté sur le schéma par un segment séparant deux individus ayant entre eux des relations de parent-descendant directs). On définit de la même façon le nombre total, n₂, de maillons entre a et j. Le nombre total de maillons sur l'ensemble de la chaîne est donc n₁+n₂. De b à i, il y a n₁-1 transmissions mendéliennes independantes les unes des autres, de c à j, il y en a n₂-2. Les probabilités pour qu'un gène de a possédé par b (respectivement c) parvienne jusqu'à i (respectivement j) s'expriment donc comme suit :

Les transmissions de a à i, d'une part, et de b à j, d'autre part, étant indépendantes entre elles, la probabilité pour que i et j aient reçu chacun un gène de a s'exprime ainsi :

          [Eq.2]

 
2) La probabilité de tirer chez i un gène provenant de a sachant qu'il en possède un est égal à 1/2 : on a une chance sur deux de tirer le gène provenant de a, et une chance sur deux également de tirer le gène homologue qui, lui, ne vient pas de a. De même, la probabilité de tirer chez j un gène provenant de a sachant qu'il en possède un est égal à 1/2. Les deux tirages étant indépendants l'un de l'autre, nous avons :

          [Eq.3]

3) Sachant que l'on a tiré deux gènes provenant de a, deux situations sont envisageables :

• Avec une probabilité 1/2, l'ancêtre a a transmis le même gène à ses deux descendants directs, b et c : les deux gènes tirés chez i et chez j sont alors copie d'un même gène ancêtre et sont donc, par définition identiques.
• Avec une probabilité 1/2, l'ancêtre a a transmis un de ses gènes à son descendant b et le gène homologue au descendant c. Par définition, la probabilité pour que ces deux gènes homologues soient identiques, et donc pour que les les deux gènes tirés chez i et chez j le soient, est égale au coefficient de consanguinité de a (F_a).

 Ainsi, nous avons :

          [Eq.4]

 
 En définitive, en reportant les équations 2 à 4 dans l'équation 1, nous obtenons :

Rappelons que la somme (n₁+n₂) est égale au nombre total de segments entre individus sur la chaîne de parenté. La somme qui figure en exposant est donc égale au nombre total (n) d'individus sur cette chaîne, et l'expression devient :