Solution  
     
1) Cas général

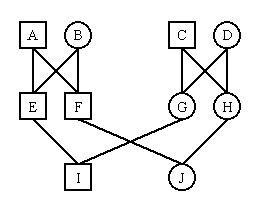
Selon la méthode tabulaire, nous avons :

E et F sont des pleins frères, G et H sont des pleines soeurs : les coefficients de parenté correspondants valent donc 1/4 (revoir le tableau récapitulatif). E et H, d'une part, G et F, d'autre part, ne sont pas apparentés entre eux : les coefficients correspondants sont nuls. Nous avons donc :

On peut aussi remarquer (méthode des chemins) que I et J ont 4 ancêtres communs non consanguins eux-mêmes (A, B, C et D), qui définissent autant de chaînes de parenté comprenant chacune un total de 5 individus. Donc,

2) Cas où les deux frères sont des vrais jumeaux

Nous reprenons l'équation en haut de cette page, le coefficient de parenté entre E et F étant modifié. Ces deux individus étant des vrais jumeaux, ils ont exactement même génotype : leur coefficient de parenté est égal au coefficient de parenté d'un individu avec lui-même, soit 1/2 (car ils ne sont pas consanguins). En définitive,

Du fait de l'identité génétique entre les deux frères, la parenté entre les deux doubles cousins germains est 50% plus élevée que dans le cas général.